連分数展開。CTFのCrypto問で必要になりました。
Python3でしか動作確認していません。
Wikipedia: 連分数をご覧ください。
コード中のexpand_to_continuous_fraction(a, b)は、下の画像でいうx=a/bとしたときの[a0, a1, a2, …]を返す関数。
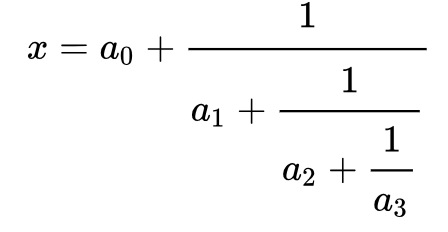
(画像はWikipedia: 連分数より引用)
コード中のcontract_from_continuous_fraction(list_a)は、「連分数の性質」とやらにより下の画像でいう[(p0,q0), (p1, q1), …]を返す関数。

(画像はWikipedia: 連分数より引用)
実行結果
>>> print (expand_to_continuous_fraction(42,11) ) [3, 1, 4, 2] >>> print ( contract_from_continuous_fraction(expand_to_continuous_fraction(42,11) ) ) [(1, 0), (3, 1), (4, 1), (19, 5), (42, 11)]
スクリプト
# -*- coding: utf-8 -*-
#a/bを連分数展開する
def expand_to_continuous_fraction(a, b):
answer = []
next_a = a
next_b = b
for i in range(100000):
c_a = next_a
c_b = next_b
if c_b == 0:
break
current_num = c_a//c_b
answer.append(current_num)
temp_next_a = c_a - current_num*c_b
next_a = c_b
next_b = temp_next_a
return answer
#連分数展開した結果をもとに、それをp/qという分数の形にしていく
def contract_from_continuous_fraction(list_expanded_continuous_fraction):
l_p =[1, list_expanded_continuous_fraction[0]]
l_q =[0, 1]
list_expanded_continuous_fraction.pop(0)
for ind_c_a, c_a in enumerate(list_expanded_continuous_fraction):
ind_pq = ind_c_a + 2
l_p.append(c_a * l_p[ind_pq -1] + l_p[ind_pq -2])
l_q.append(c_a * l_q[ind_pq -1] + l_q[ind_pq -2])
answer = []
for ind_pq in range(len(l_p)):
answer.append( (l_p[ind_pq], l_q[ind_pq]) )
return answer
print (expand_to_continuous_fraction(42,11) )
print ( contract_from_continuous_fraction(expand_to_continuous_fraction(42,11) ) )

コメント